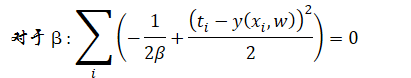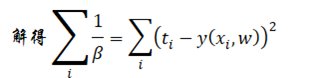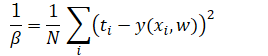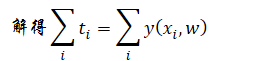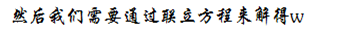本来说今天中午要写一prml，但是第一章快读完了，可是回头再一看最大后验概率，很多东西像没看一样，于是再抓起来做导图。

 

上次简略地提了下贝叶斯学派和频率学派的区别，接下来就细说一下这两派的不同的作法。

对于频率学派来说，既然把整个模型的参数看作固定的，那么要做的事情就是去估计这个参数，而一个非常常用的方法就是最大似然估计。

假设我们现在有一个曲线拟合问题，也就是说，我们有一堆相互对应的(x,t)（与书中符号一致，这里的目标值写做t而不写做y），我们希望使用通过这一堆值，去寻找到一个两者之间对应的确定关系。

首先确定一点，这些样本不会完全拟合到一个函数的（如果安全拟合的话，那就是一个矩阵或者多项式求解问题了），对于拟合不了的原因，一般使用高斯来进行捕获，即我们认为数据在整体上上符合一个给定的规则的，不能完全符合是出于设备的抖动之类的原因，将这些原因使用高斯分布来建模。

 

得到的结果差不多是这样:

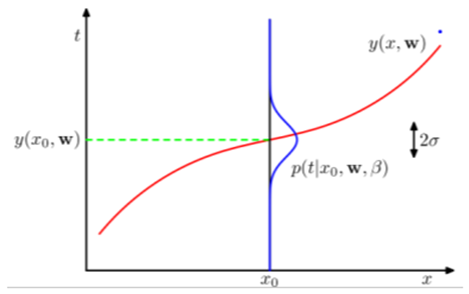
对于一个样本点而言，给定x的情况下，目标值大致出现在红线周围，并以高斯分布围绕以对应的y(x0,w)为均值。

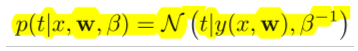
其中β是所谓的precision，其值即等于方差的倒数。

 

在建立模型之后，我们使用最大似然估计，也就是说我们要使得

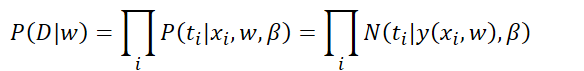
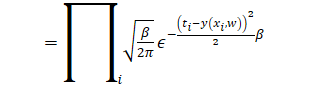
如果我们想

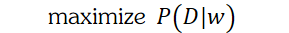
我们同样可以通过：

 

 

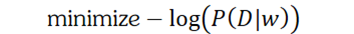
那么：

 

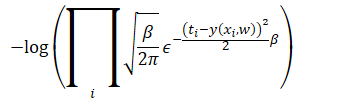
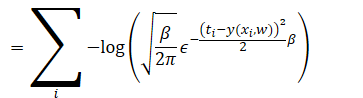
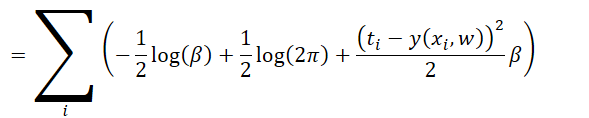
在上式中注意xi和ti是书籍量，我们的目标是求上式的极佳，上式是关于β和w的函数分别对于这个未知量求导，并令其为零。